Videos
You can get an idea of our research from the descriptions below, or from the following online talks on...
- ...quantum soliton collisions
(at I-HUB Quantum Technology Foundation, IISER Pune, 2023) - ...Rydberg Atoms in Bose-Einstein Condensed Environments[video 2]
(at ICTS Bengaluru, 2022) - ...Imaging the interface of a qubit and its quantum many-body environment
(at TGC Crest, 2022) - ...Quantum transport enabled by vibrations and non-adiabatic transitions
(at PCS Institute for Basic Science, Daejeon, 2021) - ...Quantum simulations of chemical and biological processes
(at IIP Natal, 2019) - ...Non-Hermitian matter-wave mixing in Bose-Einstein condensates
(at ICTS Bengaluru, 2018) - ...Rydberg aggregates in ultracold gases
(at ICTS Bengaluru, 2017)
Rydberg aggregates
have emerged as a versatile addition to the quantum simulation toolkit of cold atomic physics, due to their strong
long-range interactions.
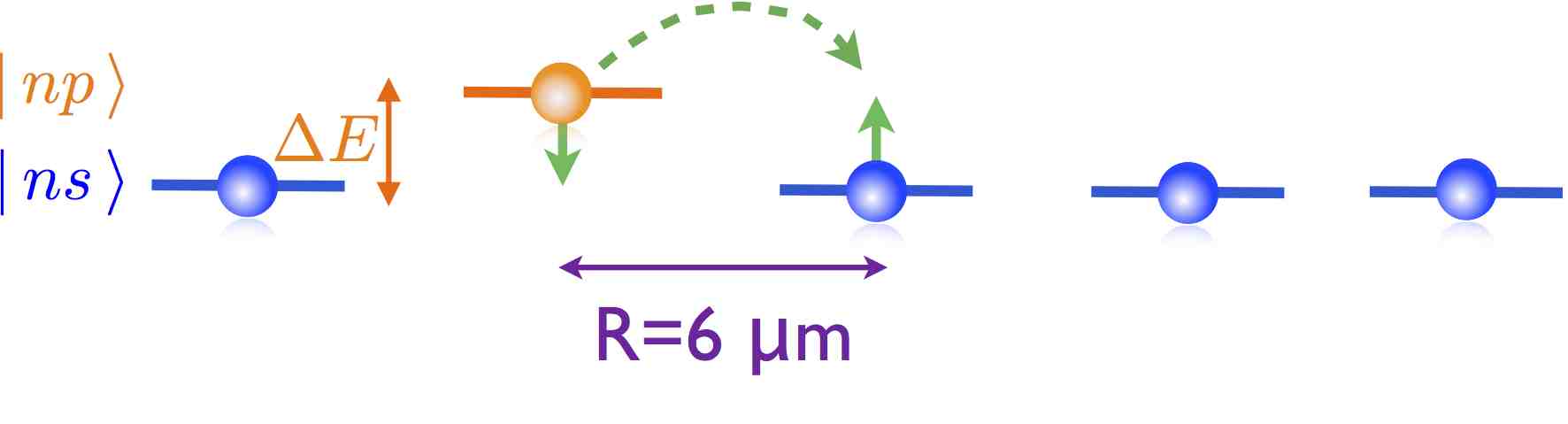
Due to these interactions, Rydberg aggregates, assemblies of few Rydberg atoms at controlled positions , exhibit collective features like excitons and accordingly excitation transport over scales of
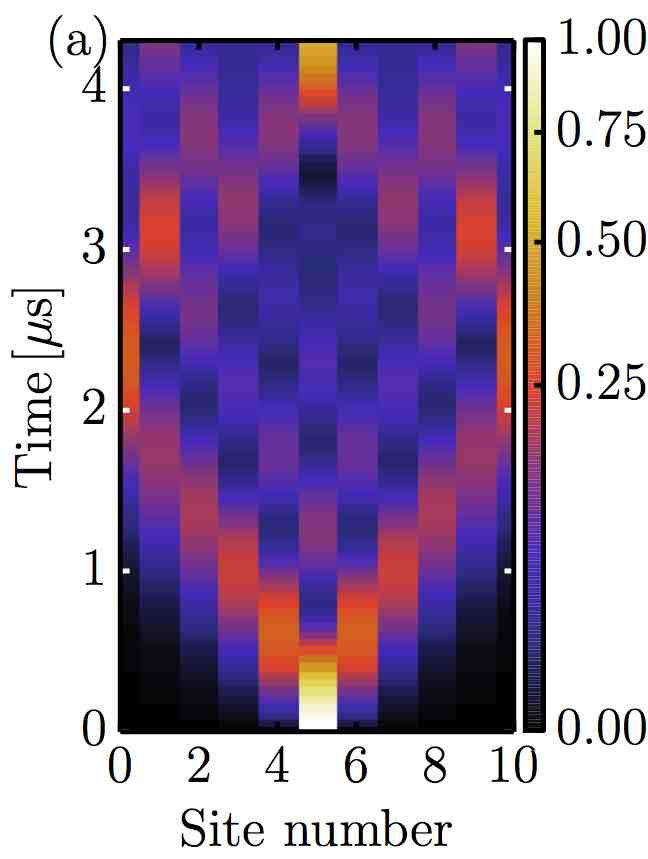
micrometers. The sketch on the left below shows a single p-excitation, migrating on a chain of Rydberg atoms in the s-state. A quantum dynamical simulation of this process is shown in the figure on the right (ballistic quantum transport).
That figure shows the probability for the single p-excitation to be on a given site of the chain as time goes on.
We can investigate three different types of Rydberg aggregates
Static Rydberg aggregates
In a static Rydberg aggregate, the atoms do not move. This could be due to trapping in an optical lattice or just very short time scales. This corresponds to the sketches shown above. There have been already the first realisations of these in experiments in Durham and Paris. These type of systems may be most interesting for the controllable realisation of long range interacting Hamiltonians from condensed matter physics.
Immersed Rydberg aggregates
In the scenario above, we would like to exploit the large lengths scales over which excitation is transported to "see" this transport directly
in an experiment. For this, it actually helps if the aggregate is located within a host cold atom cloud containing many (thousands to millions) of atoms.
This is anyway the most natural scenario in which aggregates are created. Techniques based on electromagnetically induced transparency ,
developed in Nottingham and Heidelberg,
with the latter one already demonstrated experimentally, can then be used to "see" each immersed Rydberg atom through
light absorption shadows that it casts on a camera.
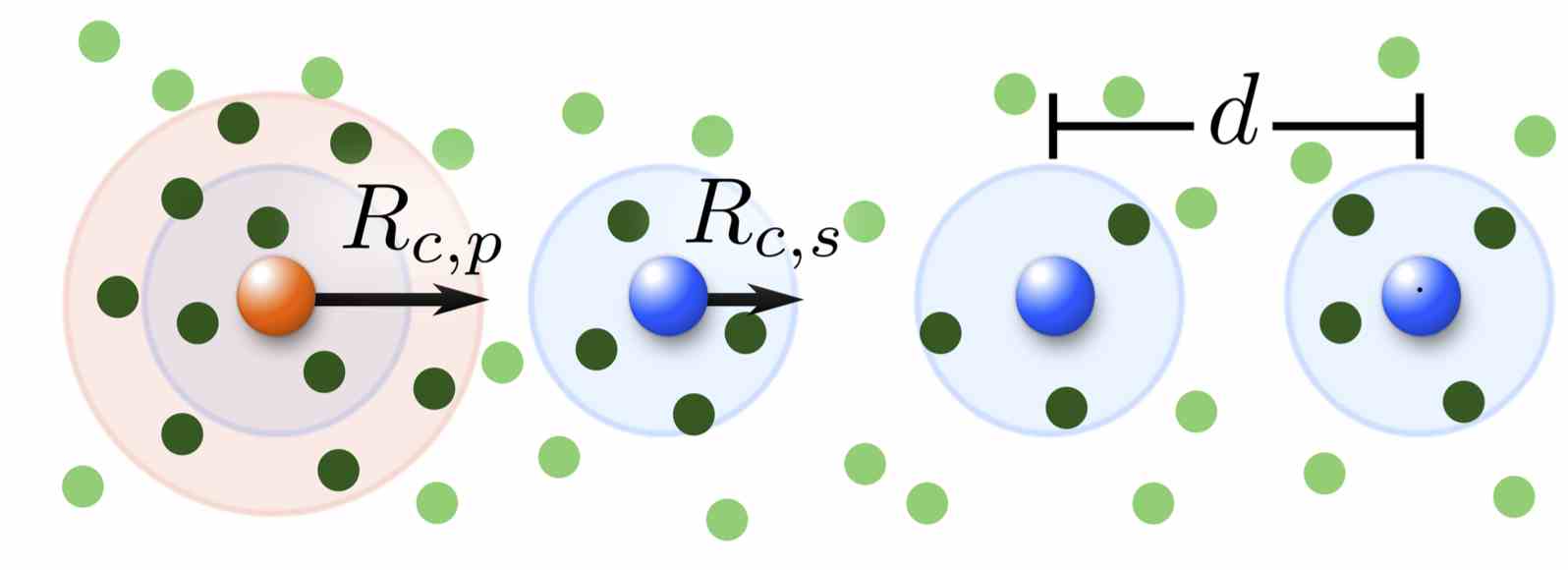
We have shown how this can be used to monitor in real time the dynamics of an immersed Rydberg aggregate, sketched on the right.
A very interesting effect of this monitoring, is that its back-action leads to energy disorder and controlled decoherence
of the aggregate [25][26], leading us to:
Quantum simulations of photosynthetic light harvesting
The energy transport on a Rydberg aggregate, sketched at the top of this page, uses the same physical mechanism (resonant dipole-dipole interactions) that also transport energy during light harvesting
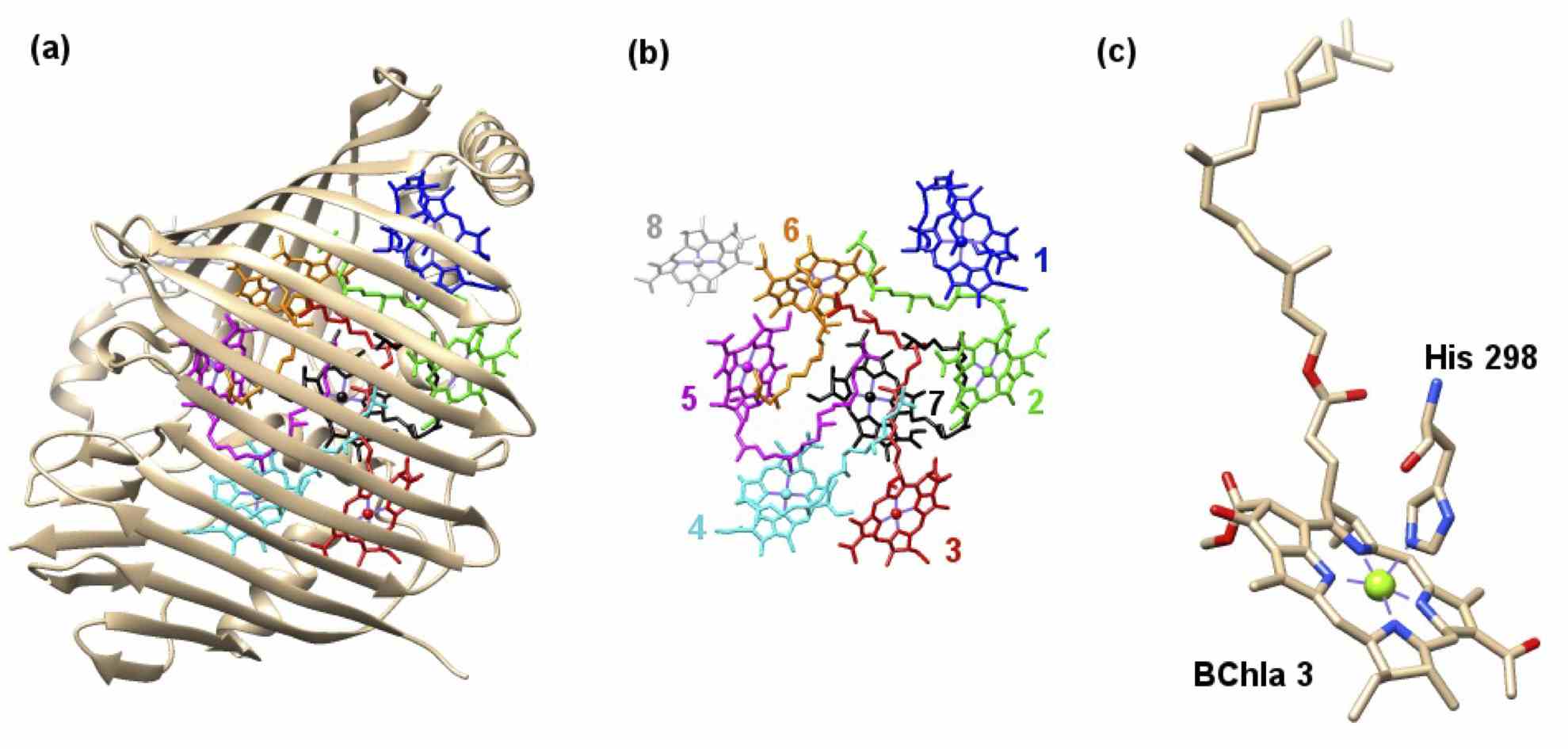
processes in nature. The figure below shows the Fenna-Matthews-Olsen (FMO) protein [28] [a], a large bio-molecule that provides a small step in the transport of light energy from the organisms "antenna" to its "reactor".
In photosynthetic energy transport the s and p Rydberg states in the cartoon at the top instead are replaced by the ground and first excited electronic states of Bacterioclorophyll molecules [c].
However, transport in the Rydberg aggregate is mostly quantum coherent and very clean and controllable. In contrast, in biological light harvesting the complicated structure of the complex bio-molecules and solvent lead to huge
environmental effects, a complicated description and strong decoherence. It is our long term goal to suggest the artificial implementation of these complications for Rydberg aggregates, which will then allow experimental
model studies (quantum simulations), in which these complications are under our control. As stated above, the simple EIT monitoring of the immersed Rydberg aggregate already gets us on the way, providing disorder and decoherence.
Flexible Rydberg aggregates

Finally, since the Rydberg atoms are much lighter than molecules, they are naturally set into motion by the excitation transporting interactions. With flexible Rydberg aggregate, we thus refer to a Rydberg aggregate in which atoms are free to move, however possibly only in some few directions, such as on a one-dimensional line. This restriction may be realised by optical trapping, such as in the sketch above, where black arrows indicate movement of the atoms. For many applications of Rydberg physics, motion of atoms induced by interaction leads to undesirable noise. Flexible Rydberg aggregates turn this noise into an asset, as we will see below.
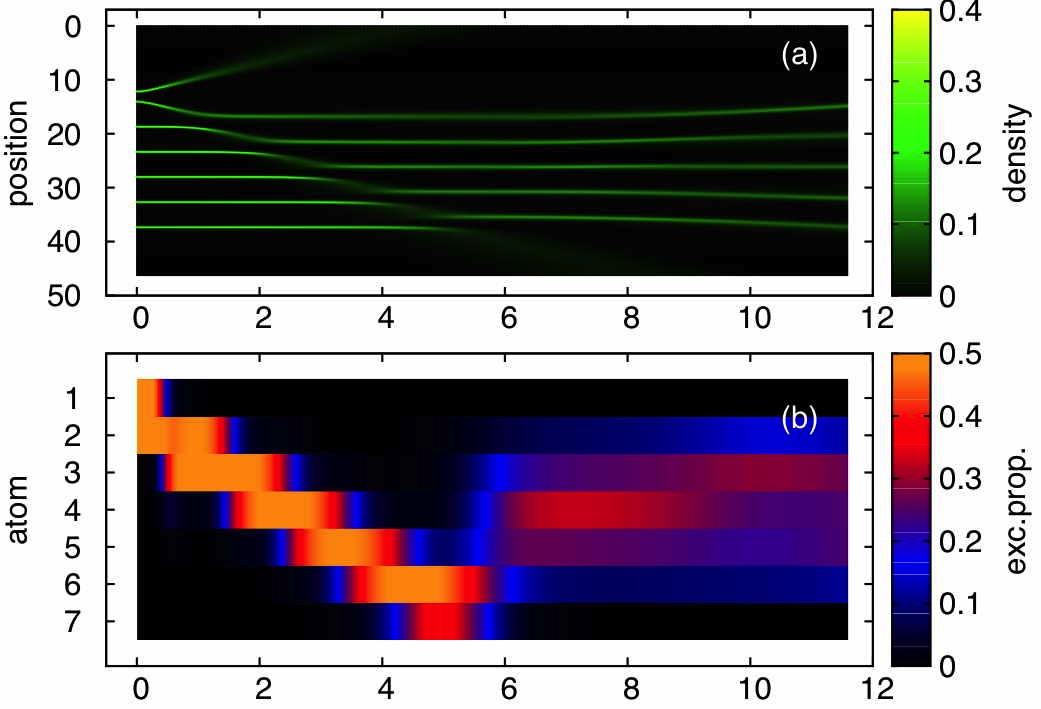
Firstly, the motion of the atoms can neatly interplay with the excitation transport shown at the top of this page, by adiabatically transporting excitation energy from one end of the chain to the other. The figure on the right shows the accompanying total atom density (top panel) and excitation probabilities per atom (bottom panel). This and articles [12][15] give more details.
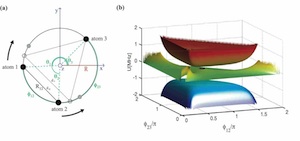
Secondly, the mechanical potentials that govern the motion of the atoms may exhibit conical intersections. The figure below right shows the geometry of three Rydberg atoms confined on a ring [panel (a)].
Their mechanical potentials (eigenstate energies) are shown as colored surfaces [panel (b)]. At the centre (equilateral triangle configuration) the red and green surfaces meet. A close zoom would show a double cone structure.
Conical intersections are interesting features of quantum chemistry, and in combination with the experimental observation capabilities provided by the
immersed aggregates above, open up the possibility for quantum simulations of chemical processes in hands-on table top cold atoms experiments.
 One could then hope to see in an experiment the crossing of the many-body system from one potential energy surface to the other, as shown in this or described in [14].
One could then hope to see in an experiment the crossing of the many-body system from one potential energy surface to the other, as shown in this or described in [14].
Finally, both of these features can be combined in exciton switches [24]. They even can be engineered entirely without any restrictions on atomic motion directions.
The latter puts them in reach of modern experiments, which can obtain more and more information on the motion of Rydberg atoms. Recent examples of these monitored, unfrozen Rydberg gas experiments
were conducted in Ann Arbor, Michigan (using field ionisation) and
Paris (using microwave spectroscopy).
Rydberg atoms
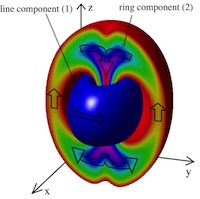
Rydberg atoms are atoms where a valence electron is excited to very high principal quantum numbers ν ~ 20 .. 200.
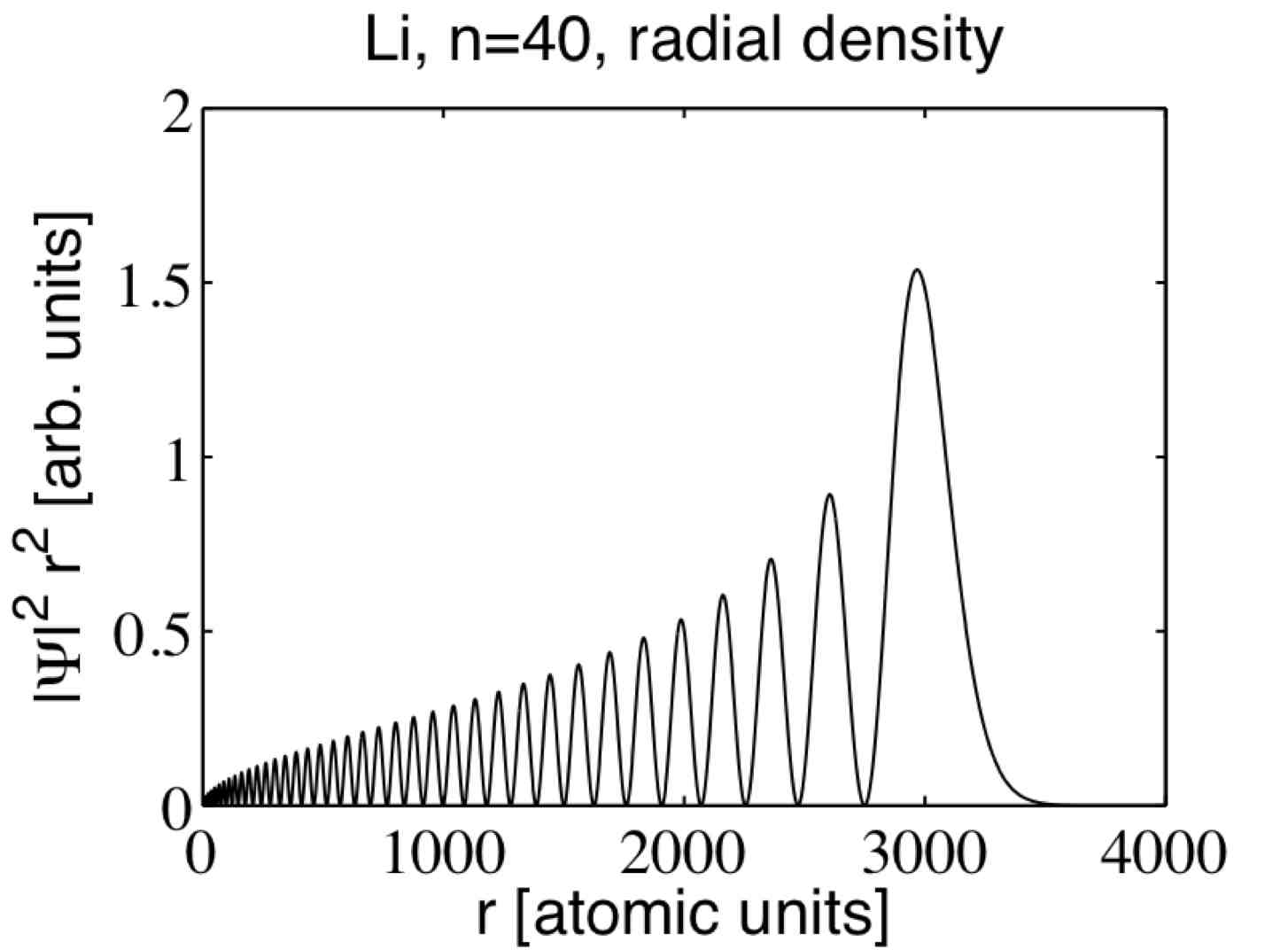 This means the electron is usually very far away from the nucleus, as seen in the image on the right,
showing where an electron in a ν= 40 state is most likely to be.
This means the electron is usually very far away from the nucleus, as seen in the image on the right,
showing where an electron in a ν= 40 state is most likely to be.
This makes these atoms huge, fragile
and very strongly interacting with one another. The far away electron also behaves very similar to the one of Hydrogen, the simplest atom, often aiding the theoretical description. Another neat feature of these electrons is,
that begin to behave more "classical" than others.
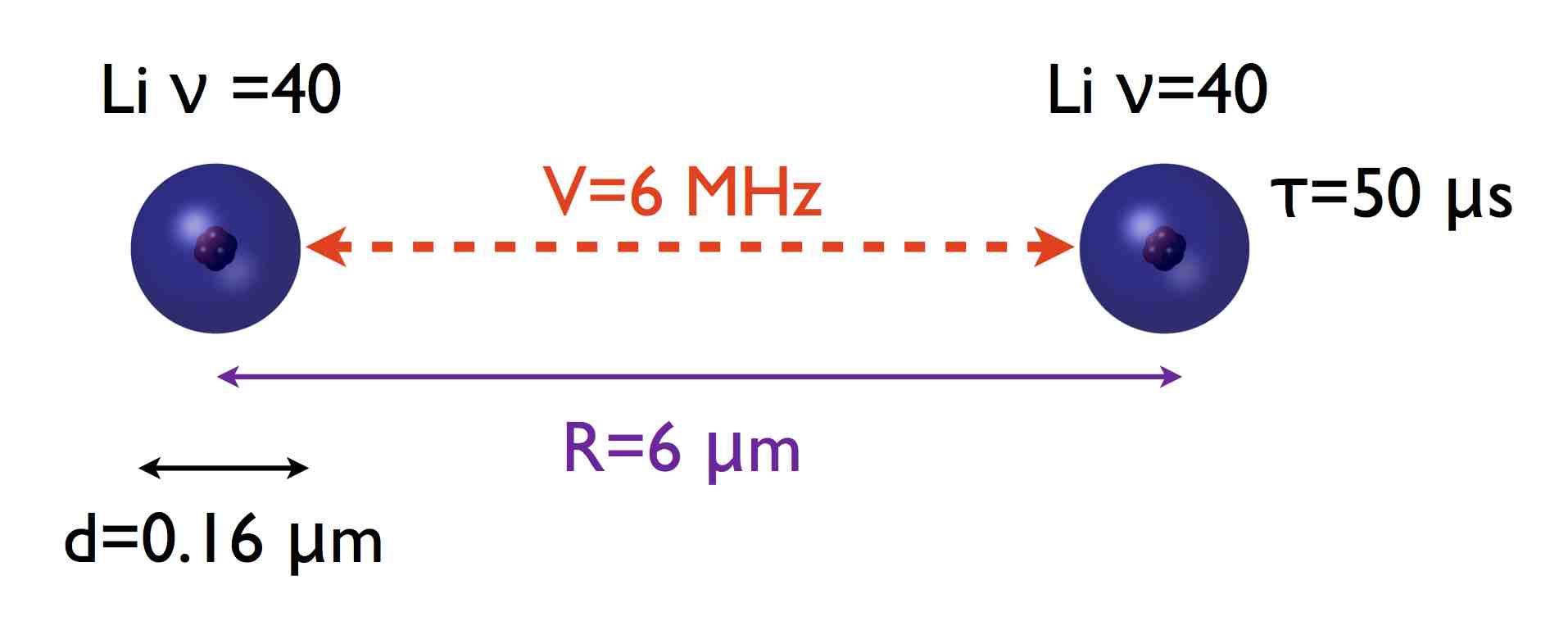
We are mostly exploiting two features of Rydberg states: Their strong long range interactions and large life-times, as shown in the sketch at the bottom.
Uses of the term "Rydberg aggregates"
The term "Rydberg aggregate" has recently been also used to describe the outcome of an actual "aggregation" process that can occur when exciting
Rydberg atoms under dissipative conditions in a cold gas. Dissipative conditions naturally occur for long times via spontaneous decay of the Rydberg state.
Experimental conditions can be tuned such that Rydberg states preferentially get excited for atoms a specific distance from an already Rydberg excited atom.
In this manner regularly arranged structures form.
We use the term Rydberg aggregates here more generally, including the above, but also atoms at experimentally chosen locations (e.g. trapping sites) such that
they are close enough to interact.
Both uses of the term "aggregate" can be seen to be borrowed from e.g. molecular aggregation. Molecular aggregates ofte self-assemble in solution (c.f. dissipative Rydberg gas),
and once assembled exhibit collective excitations called excitons and excitation transport (c.f. Rydberg aggregate designed by trapping).
Electromagnetically induced transparency
Electromagnetically induced transparency (EIT) is a technique from the field of quantum optics, exploiting multiple quantum states of atoms in a gas, as shown in the figure on the right.
Usually when we shine a laser beam on a gas of atoms, these are excited from their atomic ground-state |g> to an excited state |e>. 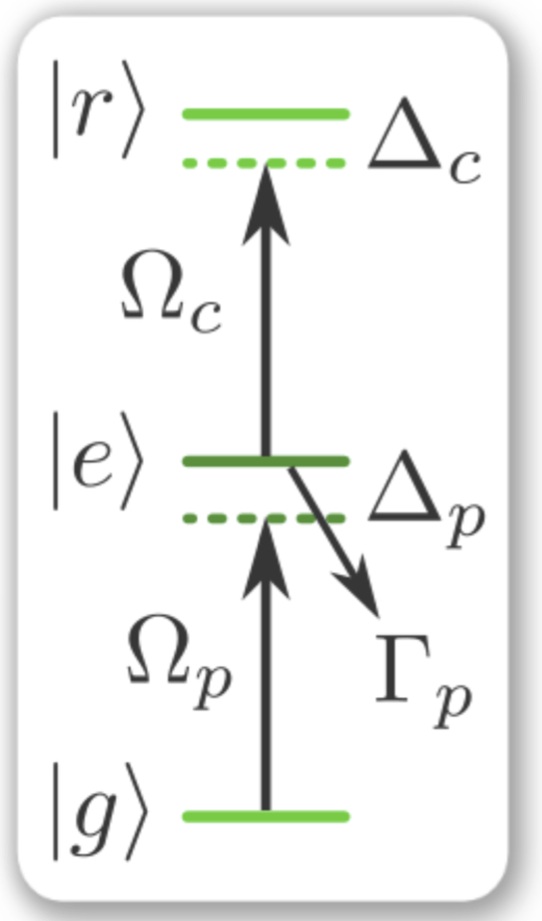 The atoms then decay back to the ground state through spontaneous emission of photons in random directions. This scatters photons out of the laser beam and causes absorption.
The atoms then decay back to the ground state through spontaneous emission of photons in random directions. This scatters photons out of the laser beam and causes absorption.
In EIT we shine two laser beams onto the gas, a probe beam (p) and a control beam (c). The scheme now, in a simple picture, exploits destructive quantum interference between the possibility
to make a transition g -> e or a transition g->e->r->e. As a consequence no atom is ever excited to the state |e>, resulting in zero absorption: The control beam has made
the gas transparent for the probe beam, hence "electromagnetically induced" transparency.
Rydberg "Newton's cradle"
The top panel of the movie shows the total density of atoms as a function of time and space. We are looking at 7 atoms on a 1D line (x). Most of them
are equally spaced, the first two sit closer together. Along the red line in the top panel, the bottom panel shows a cut through the density.
In addition, the colorcode on the bottom panel shows the probability to find our single p-excitation on the chain of Rydberg atoms,
where all others are in an s-state.
Movie credits: Sebastian Moebius
We see that the excitation is initially shared on the upper two atoms, and then transported through motion of the atoms to the bottom of the chain. Excitation here always
jumps onto the two atoms that are closest together, a consequence of adiabatic following of a quantum eigenstate. Note that both, the motion of the atoms and the jumping
of the excitation are due to the same dipole-dipole interactions.
The effect of conical intersections
For our three atoms on the ring, the movie visualizes the many-body density, which in quantum-mechanics tells us where the atoms are on the ring, and which electronic state
they are in (i.e. where is our single p-excitation). Legend for movie panels:
(top middle) This shows the atom density along the ring. We see initially three atoms in a Gaussian shaped orbital.
(bottom left) This shows the many-body density (colors) in our co-ordinate space (θ12 and θ23 are the opening angles between atom 1,2 and atom 2,3, see geometry figure on main page).
The black lines in the background are equal-energy contours of the repulsive eigenstate. This is one of the mechanical potentials, where all atoms repel.
(bottom right) The same for one other mechanical potential. This is initially not populated, and atoms do not repel here.
The two potential energies are identical (the energy surfaces meet)
at the centre of the plot (x), this is the conical intersection (CI).
(top left and top right) Please see our article or ask me.
We see that the many-body wavefunction is initially accelerated towards the CI. Upon hitting it, the central part is "sucked out" and transferred to the other surface, whereas the outer part remains on its initial surface.
These effects all have to do with the concept of quantum mechanical adiabaticity (or the absence thereof).
Rydberg Bose-Einstein condensates
Typically the time scale of dynamics in Bose-Einstein condensates (BEC), typically 1-100 milliseconds, does not match that of ultra-cold Rydberg physics, typically 1-100 microseconds.
They can however be brought to match through a technique called , where only a small fraction of Rydberg excitation is admixed to every ground state atom.
Other interesting synergies between Rydberg- and BEC physics are, that Rydberg impurities can be very controllably excited in BEC as shown in Stuttgart. This can then be used
to study losses due to Rydberg excitation or molecule formation.
We are interested in the interplay of a few Rydberg impurities in a BEC, with a Rydberg-dressed bulk BEC. 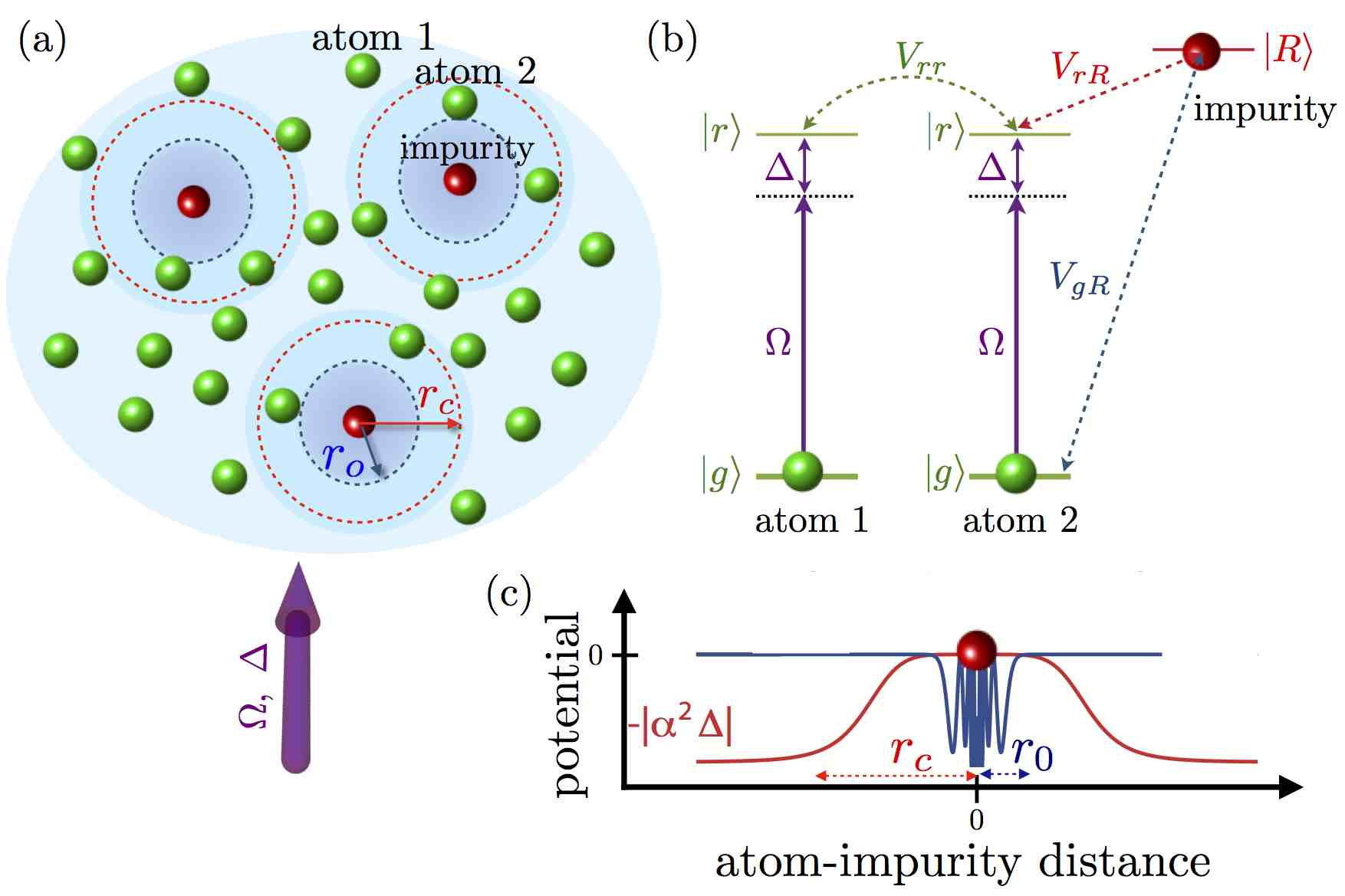 We have proposed a new kind of condensate phase imprinting
based on this setup, shown on the right [27]. The sketch shows condensate atoms (green) that experience a phase imprinting represented by the blue shades. This in turn modifies the
velocity distribution of condensate atoms and can then easily be observed experimentally. The phase imprinting should represent a versatile interface between
Rydberg atomic systems and condensates, for the example for the transfer of entanglement and thus the creation of mesoscopic Schroedinger's cat states.
We have proposed a new kind of condensate phase imprinting
based on this setup, shown on the right [27]. The sketch shows condensate atoms (green) that experience a phase imprinting represented by the blue shades. This in turn modifies the
velocity distribution of condensate atoms and can then easily be observed experimentally. The phase imprinting should represent a versatile interface between
Rydberg atomic systems and condensates, for the example for the transfer of entanglement and thus the creation of mesoscopic Schroedinger's cat states.
Rydberg-dressing
Consider two atoms at micrometer separations (atom 1,2). In their ground state |g> they do not interact at this distance. Now we shine a laser beam onto the atomic gas,
that off-resonantly couples these to a high lying Rydberg state |r>. Due to the off-resonance conditions, each atom is Rydberg excited only with a small probability.
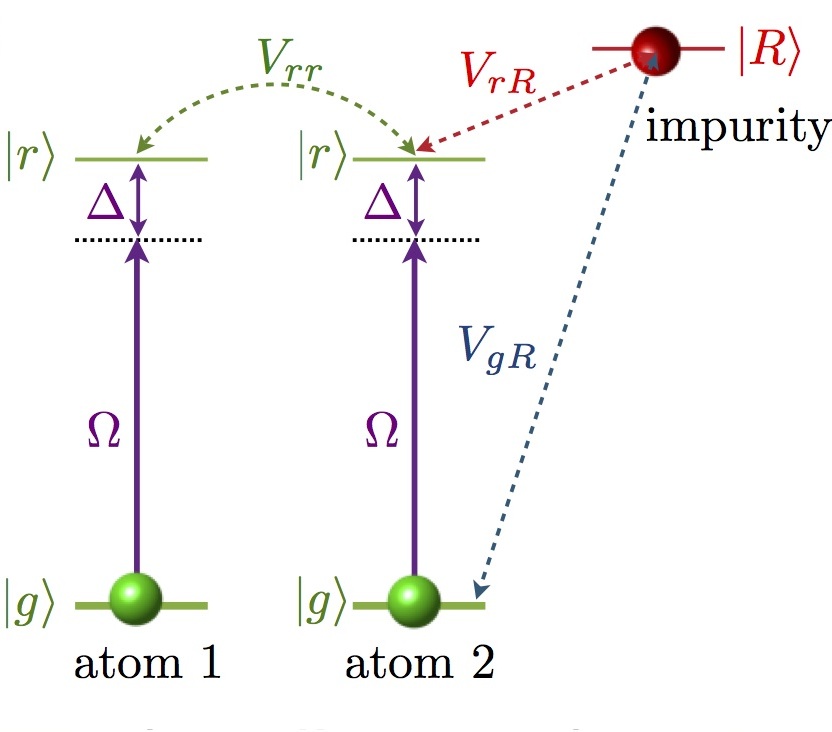 However if both of them are, they experience the huge long range interactions of Rydberg states. Quantum mechanically, each atom has to be viewed as a quantum superposition
|g> + α |e>, with α<<1. This is called a "dressed atom". These atoms now inherit the long-range nature of Rydberg atoms, albeit with a much weaker strength.
However if both of them are, they experience the huge long range interactions of Rydberg states. Quantum mechanically, each atom has to be viewed as a quantum superposition
|g> + α |e>, with α<<1. This is called a "dressed atom". These atoms now inherit the long-range nature of Rydberg atoms, albeit with a much weaker strength.
One of the first suggestions of this technique can be found here,
and neat applications in these
articles. The concept can also be applied to excitation transport [13][18].
We are additionally interested in the interplay of the phenomenon above (atoms mostly in the ground-state) with FEW really Rydberg excited atoms (100% in the Rydberg state, red ball).
Quantum Optomechanics
 studies the interplay of mechanical motion, such like vibrations of a mirror, and optical driving by laser fields in the quantum mechanical ergime. One of the appeals is that the quantum mechanical
regime is often reached for rather "large", mesoscopic sizes of the mirror. Devices based on this then offer applications in fundamental physics, such as gravitational wave detection, and newly emerging quantum technologies.
studies the interplay of mechanical motion, such like vibrations of a mirror, and optical driving by laser fields in the quantum mechanical ergime. One of the appeals is that the quantum mechanical
regime is often reached for rather "large", mesoscopic sizes of the mirror. Devices based on this then offer applications in fundamental physics, such as gravitational wave detection, and newly emerging quantum technologies.
Due to the huge variety of nano-mechanical oscillators that can be engineered, these cover many orders of magnitude in masses and frequencies. Highly excited Rydberg states show a similarly diverse range of frequency gaps,
suggesting the fruitful combination of the two fields. To this end we have begun investigating the coupling of an oscillating mirror with Rydberg atoms, with the long term plan of quantum control of the mirror.
[Image courtesy of Manuel Sanz-Mora, via Adrian Sanz-Mora.]
Quantum Optomechanics
The paradigmatic setup of quantum optomechanics is shown below. An optical cavity with resonance frequency ωc is driven by a laser with frequency ωL.
One end mirror of the cavity is free to vibrate. Now the motion of the mirror affects the amplitude A of light stored in the cavity by changing the resonance frequency of the
cavity. In turn the amplitude A affects mirror motion through radiation pressure on the mirror.
The resulting feedback loop can, for witty choice of parameters, be used to cool the mirror to its quantum mechanical vibration ground state.
Besides the standard example above, a huge variety of mechanical element- and electromagnetic field type combinations are possible.

Bose-Einstein condensates
 Bose-Einstein condensates (BECs) are an excellent system to study complicated phenomena emerging from well understood microscopic physics.
They also allow very extremely fine experimental control over system parameters.
For our studies of them our workhorse is condensate mean field theory, but we also consider quantum corrections in the Hartree-Fock-Bogoliubov and truncated Wigner theories.
Bose-Einstein condensates (BECs) are an excellent system to study complicated phenomena emerging from well understood microscopic physics.
They also allow very extremely fine experimental control over system parameters.
For our studies of them our workhorse is condensate mean field theory, but we also consider quantum corrections in the Hartree-Fock-Bogoliubov and truncated Wigner theories.
The list of our topics is diverse:
- We investigated possible quantum effects in condensate collapse due to attractive interactions ("Bosenova"). [1][3]
- We have found requirements for the experimental creation of Skyrmions. These are topological solitons, which for example took part in the recent story of prediction, discovery and dispute of the pentaquark in particle physics. [2]
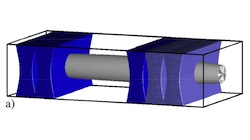
- We proposed the stabilisation of ring vortices using optical tunnels through which the BEC flows. [4]
- We studied quantum effects on the genesis of bright solitons in the wake of a condensate collapse. [9]
- We surveyed prospects of studying the quantum-classical transition in quantum chaos using condensates in magnetic microtraps. [16]
- We analysed Kerr-squeezing in Bose-Einstein condensates and homodyne methods for its detection. [6]
Analogue gravity
 It has been realized that the same laws of nature govern quantum particle propagating in a curved space-time (such as near a black hole) and sound-waves propagating in a moving, cold quantum-fluid.
Roughly speaking, the location where the background flow velocity turns super-sonic represents a point of no return for the sound wave, just as the event horizon of the black hole does for the particle.
It has been realized that the same laws of nature govern quantum particle propagating in a curved space-time (such as near a black hole) and sound-waves propagating in a moving, cold quantum-fluid.
Roughly speaking, the location where the background flow velocity turns super-sonic represents a point of no return for the sound wave, just as the event horizon of the black hole does for the particle.
Bose-Einstein condensates are a promising fluid in which this could be exploited, due to their extremely low temperatures and precise experimental control over them.
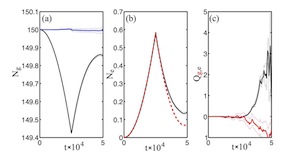
One ultimate goal would be the experimental verification of (analog) Hawking radiation. We have pointed out the importance of carefully considering classical and quantum effects due to
three-body losses for any such endeavour. [5][7]
Recent experiments in Haifa have progressed significantly towards the goal of observing spontaneous analog Hawking radiation, by detection their amplified counterpart in a
"black-hole laser".
Stochastic quantum field theory
 The Hilbert-space size problem usually preventing first-principles simulations of quantum many-body systems can be overcome for short times using stochastic gauge methods.
The essential trick here is the mapping of quantum-correlations to correlations of complex random variables in a large ensemble. It allows the reduction of the computational size of an N-particle, M-mode problem from the
quantum mechanical M^N to merely M, albeit with the need of treating a large stochastic ensemble.
The Hilbert-space size problem usually preventing first-principles simulations of quantum many-body systems can be overcome for short times using stochastic gauge methods.
The essential trick here is the mapping of quantum-correlations to correlations of complex random variables in a large ensemble. It allows the reduction of the computational size of an N-particle, M-mode problem from the
quantum mechanical M^N to merely M, albeit with the need of treating a large stochastic ensemble.
The available simulation time is limited by onset of exponential increase of the simulation's noise content. This time-span can be lengthened, by the use of drift and adaptive diffusion gauges,
which we aim to generalize to systems with long-range interactions, most notably Rydberg atom assemblies.


